|
Lipid Membrane Mechanics
All
biological membranes are composed of amphiphilic lipid molecules
which self-organize to form fluid bilayers. Considering these
membranes serve a variety of mechanical and organizational roles
within a cell, it is of some interest to understand their mechanical
properties. Arguably the two most important mechanical properties
of a membrane are its area stretch modulus and bending modulus
(presuming it is a linear elastic material). These
membranes exhibit some very unique properties in that they are
fluid in-plane, hence any localization of surface tension quickly
equilibrates with the rest of the membrane. Our goal in this
experiment was to measure the area strech modulus of a DOPC bilayer
(dual 18 carbon chain).
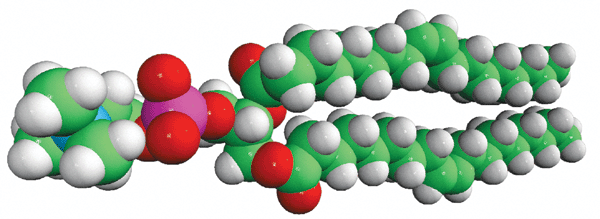
Structure
of DOPC (Avanti Polar Lipids)
Testing
the stretch properties of a bilayer require that we make giant
unilamellar vesicles (GUV's). These vesicles are formed by depositing
a thin layer of pure lipid dissolved in cholorform onto a conductive
glass substrate. The lipid layer is dried and then hydrated in
the desired aqueous buffer. This hydrated lipid layer is then
subjected to an oscillating electric field, and over the course
of a few hours, GUV's form.
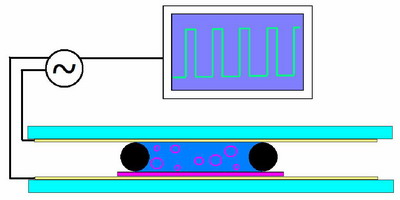 
A
rough sketch of the electroformation chamber. The purple coating
on the bottom represents the lipid, electrical contacts are attached
to the conductive substrate on both sides of a chamber filled with
aqueous buffer and the oscillating field is applied across the chamber.
The results are
shown in the picture to the right.
Once
formed, the GUV's are diluted significantly and put into a temperature
controlled microscope stage. In this stage they will be manipulated
with a micropipette, which when suction is applied, deforms the
GUV's in a well characterized way.

Diagram showing the basic setup for an area stretch experiment.
Vesicles are imaged on an inverted, epi-fluorescence microscope.
Finding
the
percent area change (areal strain) and surface tension as a function
of suction pressure reduces to measuring simple geometric features
of the GUV.
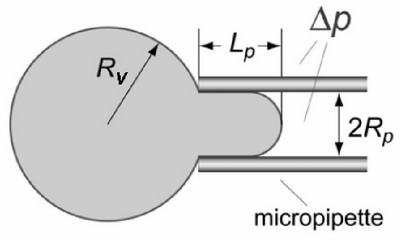
Knowing
the geometric features shown on this diagram
and the suction pressure allows one to calculate the areal
strain and surface tension.
As
the suction pressure rises the membrane stretches and the surface
tension increases, until finally the membrane ruptures. It can
be shown that the GUV maintains constant volume over the course
of the experiment (to within ~1%).
|

