|
Our purpose in this experiment is to estimate the surface tension of liposomes and the line tension between lipid membrane domains. B riefly , we applied a known pressure on the vesicles, and then measured the geometry of the structure . We are told this might be the first report on direct measurement of line tension of liposomes in the world, which makes this project very exciting.
{top}
Introduction
Lipid bilayer is lamellar arrangement of lipids in biological membranes. It is formed by lipids of a long hydrophobic tail (14 to 24 carbon atoms) and a polar head. Since water is polar, the heads will try to be with water, and the tails will avoid the water, forming structures like this:
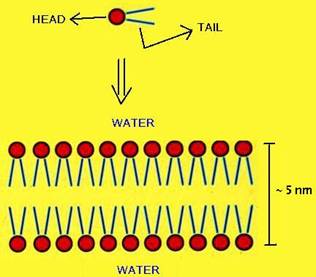
The aqueous environment inside and outside the bilayer prevents the lipids from escaping, but nothing stops these molecules from moving about and changing places with one another within the plane of the bilayer. Therefore, it behaves as a two-dimensional fluid, which is crucial for the cell membrane function. Besides this high degree of lateral motility, lipid molecules rotate very rapidly about their long axis, due to the temperature. In fact, as we could observe in our experiment, as the temperature increases, so does the fluidity of the bilayer. Another type of movement is the transverse movement (flip-flop), but it is very rare.
For this experiment, we built the particles we built are called liposomes. Liposomes are closed spherical vesicles that surround an aqueous interior. They are artificial, consist of a single bilayer of phospholipid and can be used to deliver drugs or genetic material into a cell. What makes this possible is that they can fuse with other bilayers, such as the cell membrane, delivering their contents.

Liposome
Lipid bilayer membranes play an important role in cell function. Cell membranes have the appropriate permeability barrier, establishing a distinction between the inside and the outside of the cell. The lipid bilayer from the cell membrane helps to sustain osmotic gradients across the membrane, blocking the passage of almost all water-soluble molecules, due to the hydrophobic interior of the bilayer.
There are also other biological processes in which bilayers are crucial, such as endocytosis (phagocytosis, pinocytosis) and ion channel regulation.
Line tension at the boundary between coexisting lipid membrane domains may have very important biological functions. It has been proposed to play important roles in budding, fission and membrane deformation. Theoretical estimates of the line tension are on the order of 10^ -11 N for system far from critical points of the lipid phase diagram. It will vanishes at critical points.
{top}
I. Surface Tension
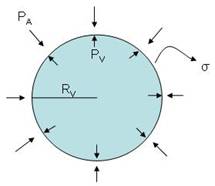
Consider the following liposome:
where:
- P A is the atmospheric pressure
- P V is the pressure inside the vesicle
- R V is the radius of the vesicle (considering the vesicle an sphere, with flat surface)
- σ is the surface tension with units: J/m ² or N/m
So the energy of this system is
E = σA-ΔPV,
where A is the surface area of the sphere and ΔP = PV – PV. Then
E = σ4πR2-ΔP4/3πR3
We have ΔP fixed (nothing leaves the interior of the vesicle, and P A does not change) and σ depends on the composition of the vesicle. So what is the radius R?
To find that, we have to minimize the energy with respect to R:
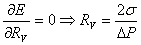
This is called Laplace relation.
In this case, we assumed that σ and PV are constant. We can get the same result if we look at an infinitesimal region of the vesicle
without the assumption that σ and PV are constant :
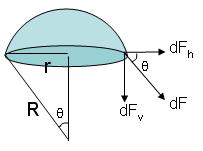
Since the vesicle is in equilibrium (it is not shrinking or expanding), the total force over any region must be zero. The forces acting on the vesicle are 1) the one due to the difference between the inner and outer pressure, and 2) the one due to the surface tension.
- If we approximate the spherical region to a circular region of radius r, the force is just F T = Δ P( π r ² )
- We can sum all the infinitesimal forces dF acting on each small piece of length dx. But
σ = dF/dx and dF = σ dx
Since the components dF h cancel, we can integrate over dF v and use the relation above to get
FT = σ 2πr sinθ
Therefore,
ΔP (π r2) =σ 2π r sinθ ,
where
sinθ = r/R
Finally,
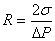
{top}
II. Model
O ur experiment consists of a micropipette applying some pressure over the surface of such a sphere that contains a certain domain:
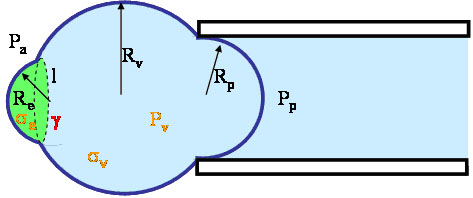
Using the relation we derived for the radius, we can find three equations:
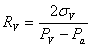
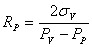
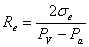
where we assumed that the surface tension is constant over the vesicle, and different on the domain.
We know R v , R p, R e, P a (we can measure) and P p (we control). So we can solve the equations above for our unknowns and obtain:
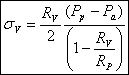
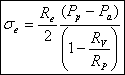
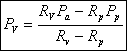
Another parameter that we are more interested in is the line tension between the domain and the liposome. We use again the argument of equilibrium of forces to get the equation for the line tension γ :
(σv-σe)Ae = γl
Using the solutions above, we get
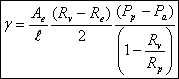
It is easy to see if these equations are wrong, just by checking the sign (everything should be positive).
{top}
Procedure
The lipid mixture we used in our experiments is 35% dioleoyl-phosphatidylcholine (DOPC), 35% dipalmitoyl -phosphatidylcholine (DPPC) and 30% chloroform. Also included is 0.8% DPPE-Liss Rhodamine for domain labeling.
1. The unilamellar liposomes we used were made by electroformation.

-
Everything should be cleaned with DI water and ethanol
-
With a 10ul glass syringe, we applied on the slide a 2-3ul droplet of the solution of lipid and chloroform in the center of the ITO slide
-
Under the right angle, it is possible to see a green reflexion of the light
-
We used two types of lipids so that we could see two different phases on the surface of the vesicle
-
Immediately after that, the device was placed in a vacuum desiccator for about 1 hour, to let the solution dry
-
After that, we placed a buffer solution in the O-ring
-
Then we put the top half of the chamber on using the alignment pins
-
Carefully we took it to the microscope and placed the chamber there
-
After attaching the BNC connector to the chamber, we set a voltage no more than 5V (more than that could damage the ITO coating) and a frequency of about 10Hz
-
We waited for about 3 hours to have the liposomes formed (the exact mechanism of such formation is yet not very clear)
-
These liposomes are good for some hours (about 12 hours, in our experiments
2. After the formation, we made a solution of 1:200 of the liposomes in glucose. We had to cut the tip of the pipette we used, because the size of its opening was about the size of the vesicles, and they could get stuck there or be damaged.
3. We had to make also the micropipettes that we used
-
First, we got a long capillary and cut it into pieces (about 10 cm long)
-
Each smaller capillary was placed in the Sutter P-97 Micropipette Puller, an equipment that heated the center of the capillary and pulled the edges, breaking it in half. We only used the right half, because the tip from the left half was deformed

Sutter P-97 Micropipette Puller
-
Now the tip of the capillary was thin enough, but it was closed, so we had to open it. To do this, we chose the capillary that had the straightest tips
-
Using another equipment, we inserted the tip of the capillary into a heated glass sphere (about 1mm in diameter) and let the sphere cool down – a foot pedal controlled the heating device
-
Then we pulled the capillary, breaking it in the tip. Although we had a hole in the capillary, the edges were deformed. So we inserted it again into the heated sphere
-
Glass from the sphere entered the capillary and then we let everything cool down again. A light knock on the table was enough to break the tip once more
-
This process made the tip now too sharp for the liposomes, so we just approached the tip to the heated sphere, without touching it, to make the edges smoother
-
We cleaned the micropipette with ethanol, and used a syringe to check if water could go through the micropipette and get rid of any bubble in it, by filling it entirely with water
4. With the micropipette ready, we placed it in the microscope, avoiding bubbles.
5. We inserted it into the opening at the center of the chamber and placed it in the field of view of the microscope, focusing on the pipette.
6. Then we placed a solution of BSA (Bovine serum albumin) within the opening, avoiding bubbles
7. After 15 minutes, we removed the BSA with a Kim Wipe and replaced it with water, letting it there for 5 minutes
8. We removed the water and placed the solution with the liposomes in the opening, after gently mixing the solution .
9. We set a temperature for our experiment between 10 oC and 20 oC and waited for about 5 minutes, to let everything reach equilibrium and have everything ready. For most of the time, we keep the temperature at 18 o C .
10. Using the micropipette, we tried to capture vesicles, by placing the pipette and the vesicle we want in the same plane. Normally the vesicles were at the bottom of the solution and were aligned almost vertically.
11. Using a device that can vary pressure based on the height of a column of water, we captured vesicles that had large domains, so that we could calculate the line tension between the lipids and the surface tension for each of the lipids, according to our model.
{top}
We write a simple matlab program to process the images and calculate the unknowns including the line tension. Each time the program is executed, one image is processed. The program first prompts for the image. Then it converts the image from 16 bits to 8 bits and performs appropriate scaling on it. Next a image is displayed and a getline function is evoked to let user select the curve for Rv calculation. The results are saved as coordinates in two vectors. We use the zoom in from Tools menu before the selection. This process repeats for Re, Rp and l calculation. For l, only two points are selected. The curvatures are calculated with formula as below with difference operation:
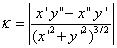
And the radius is just the inverse of curvature. Finally all the unknowns are calculated as in boxed equations in model section.
{top}
We chose eight images with better quality than the rest and processed them.

03-02-06_01 |

03-02-06_02 |

03-02-06_12 |

03-02-06_13 |

03-02-06_14 |
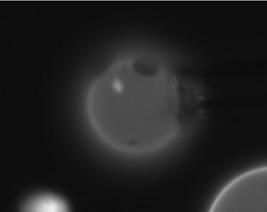
02-24-06_10 |
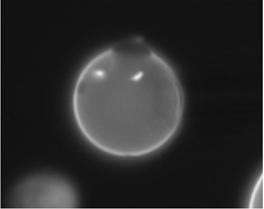
02-24-06_11 |
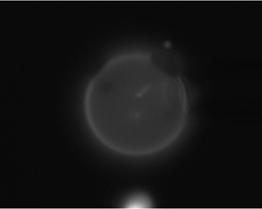
02-24-06_12 |
Below is a table that summarizes the results with calculated average and standard deviation.
Image number |
Pressure Reading (Labview units) |
Surface Tension σ v (10-6 N/m) |
Surface Tension σ e (10-6 N/m) |
Inner Pressure P v (105 Pa) |
Line Tension γ (10-11 N) |
03-02-06_01 |
50 |
9.8512 |
2.6244 |
1.01 |
1.2314 |
03-02-06_02 |
50 |
23.283 |
9.7889 |
1.0101 |
3.0206 |
03-02-06_12 |
25 |
10.538 |
8.0578 |
1.0101 |
0.48618 |
03-02-06_13 |
50 |
18.961 |
5.1839 |
1.0101 |
1.7665 |
03-02-06_14 |
30 |
21.69 |
7.7705 |
1.0101 |
1.783 |
02-24-06_10 |
50 |
24.365 |
9.2094 |
1.0101 |
1.7286 |
02-24-06_11 |
30 |
6.043 |
2.2648 |
1.01 |
0.5959 |
02-24-06_12 |
30 |
20.045 |
7.3745 |
1.0101 |
1.8025 |
Average |
- |
16.84703 |
6.53428 |
1.01007 |
1.55184 |
Std |
- |
6.98534 |
2.86963 |
4.6291x10-5 |
0.80205 |
So our result suggests that the line tension can be directly measured and for the lipids we are using, its value is:1.55184 ± 0.80205 x 10 -11 N. The value matches very well with the magnitude of order prediction of 10 -11 N. (Baumgart, T., Hess, S. T. and Webb W. W., Nature, 425, 821-824, 2003 )
{top}
During the experiment, we observed some problems that could be avoided. As we didn't have much practice with the “vesicle hunting”, it took some time for us to find the vesicles that interested us. It was hard to place the micropipette and the vesicle we wanted in the same plane. Because of this, the vesicles were getting aged and started to “dismantle” , so we couldn't get better pictures that we wanted.
One great problem was the micropipette. Again the practice would have helped us. As we captured the vesicles, sometimes it was clear that there was liquid going in the pipette since we observed the lipid layer near the entrance of the micro-pipettes vibrates. This usually means that the tips of our micro - pipettes were not flat and smooth enough to form a good seal with the liposome . One way to test that is to place one electrode inside the micro-pipette and another electrode outside. If giga Ohm resistance is measured when negative pressure is applied inside, then it means the sealing is really good.
To get a good estimate of the three curvatures, it is beneficial to focus on the latitude so that the image is most sharp. But normally the domain will not be in right focus. Sometimes we have to wait for a long time and snap an image when the domain moves into focus. Maybe some algorithm can be developed to correct the effects.
Another issue was that the domains were not easily visible because the background was dark and so was the domain. This makes image processing more difficult. For data processing part, because of the quality of the data, we could not find a good way to do edge detection for all the boundaries automatically in matlab. The black domain and the dark background make it very hard to draw a boundary. In the end, we picked up the boundary with naked eye in matlab. The arbitrary nature of this process definitely introduces large errors. This could be avoided if we labeled each type of lipid with a different fluorophore.
{top}
Acknowledgment
We would like to thank our TA, Tristan Ursell, who built the testing system, designed the experiment, spend time with us and provide us suggestions for image processing.
{top}
|